PBR

BRDF

bidirectional reflective distribution function(双向反射分布函数)
现在已经有很好几种BRDF都能近似的得出物体表面对于光的反应，但是几乎所有实时渲染管线使用的都是一种被称为Cook-Torrance BRDF模型.

链接地址

Cook-Torrance BRDF兼有漫反射和镜面反射两个部分：

镜面反射函数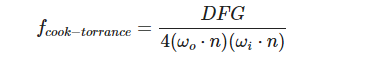

三个函数分别为法线分布函数(normal Distribution Function)，菲涅尔方程(Fresnel rquation)和几何函数(Geometry function)
法线分布函数：估算在受到表面粗糙度的影响下，朝向方向与半程向量一致的微平面的数量。这是用来估算微平面的主要函数
几何函数：描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线
菲涅尔方程：菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率

法线分布函数

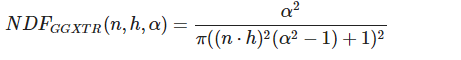
 float DistributionGGX(vec3 N, vec3 H, float roughness)
{
    float a = roughness*roughness;
    float a2 = a*a;
    float NdotH = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;

    float nom   = a2;
    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
    denom = PI * denom * denom;

    return nom / denom;
}

几何函数

 float GeometrySchlickGGX(float NdotV, float roughness)
{
    float r = (roughness + 1.0);
    float k = (r*r) / 8.0;

    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}

float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2 = GeometrySchlickGGX(NdotV, roughness);
    float ggx1 = GeometrySchlickGGX(NdotL, roughness);

    return ggx1 * ggx2;
}

菲涅尔方程

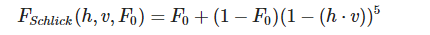
 vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
    return F0 + (1.0 - F0) * pow(clamp(1.0 - cosTheta, 0.0, 1.0), 5.0);
}

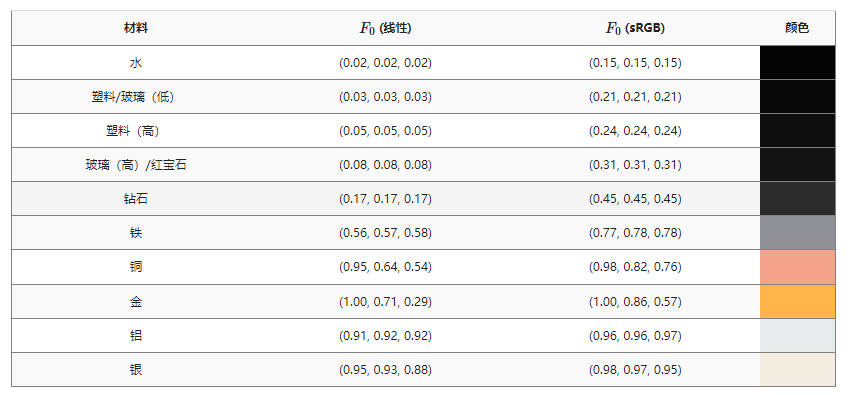
Cook-Torrance反射率方程

最后的函数

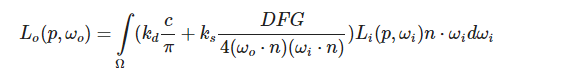
因为菲涅尔方程直接给出了kS
， 我们可以使用F表示所有打在物体表面上的镜面反射光的贡献。 从kS
我们很容易计算折射的比值kD
：

// kS is equal to Fresnel
vec3 kS = F;
// for energy conservation, the diffuse and specular light can't
// be above 1.0 (unless the surface emits light); to preserve this
// relationship the diffuse component (kD) should equal 1.0 - kS.
vec3 kD = vec3(1.0) - kS;
// multiply kD by the inverse metalness such that only non-metals 
// have diffuse lighting, or a linear blend if partly metal (pure metals
// have no diffuse light).
kD *= 1.0 - metallic;